| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- pm2 업데이트 에러
- Learning React
- nuxt universal rendering
- component is already mounted please use $fetch instead.
- d3 지도
- cloud firestore id auto increment
- d3 지도 툴팁
- d3 지도 확대/축소
- img 태그 sizes
- 헌혈유공패 은장
- reflow
- git
- firebase id 자동
- vue3 drag and drop
- repaint
- pm2 버전 충돌
- 함수형 프로그래밍
- ToDo
- 이미지 성능 최적화
- d3 지도 타입스크립트
- $fetch
- vuedraggable
- img 태그 srcset
- 인터넷 거버넌스
- 웹 퍼포먼스 도구
- in-memory pm2 is out-of-date
- commonjs와 ecmascript modules(esm)
- vue composable 함수
- vue draggable 차트 안나옴
- vue 컴포저블 함수
- Today
- Total
빵 입니다.
삼각함수 본문
삼각비를 각에 대한 함수로 나타낸 것으로
삼각형의 각과 변의 길이를 연관시킨 각에 대한 함수
직각 삼각형 => 삼각비 존재
모양이 다른 직각 삼각형이여도 θ 값이 같다면 삼각비는 같다.
= 모든 직각 삼각형의 삼각비는 같다.
= 비를 그대로 유지
대변
다각형에서, 한 변이나 한 각과 마주 대하고 있는 변.
빗변
직각 삼각형의 직각에 대한 변. 비스듬히 기울어진 변.
인접변
한 변을 공유하고 같은 평면에 놓여 있지 않은 두 평면.
두 집합 X, Y에 대하여 X의 임의의 원소 x가 Y의 오직 한 원소 y에 대응될 때, 이러한 관계를 함수라고 한다.
이때 X를 이 함수의 정의역이라 하고, Y를 이 함수의 공역이라고 한다.
따라서 함수의 치역은 공역의 부분집합니다.
역함수
삼각 함수의 역함수의 경우에는 함수들을 y=x에 대해 대칭이동 하면된다.
하지만 범위는 정해줘야 한다.
1. 직각 삼각형에서의 삼각함수
사인(sine), 코사인(cosine), 탄젠트(tangent)
sin A = 대변/빗변 = a/c
cos A = 인접변/빗변 = b/c
tan A = 대변/인접변 = a/b
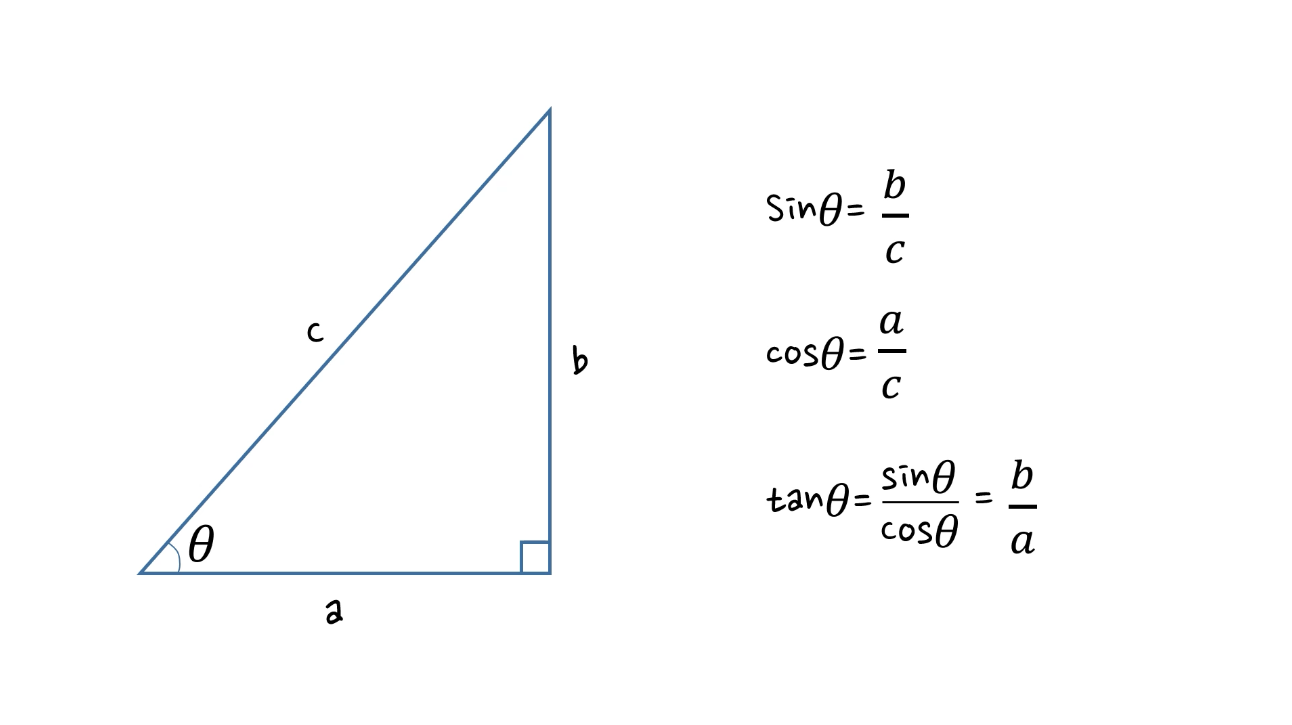
역함수
코시컨트(cosecant), 시컨트(secant), 코탄젠트(cotangent)
csc A = 빗변/대변 = c/a
sec A = 빗변/인접변 = c/b
cot A = 인접변/대변 = b/a
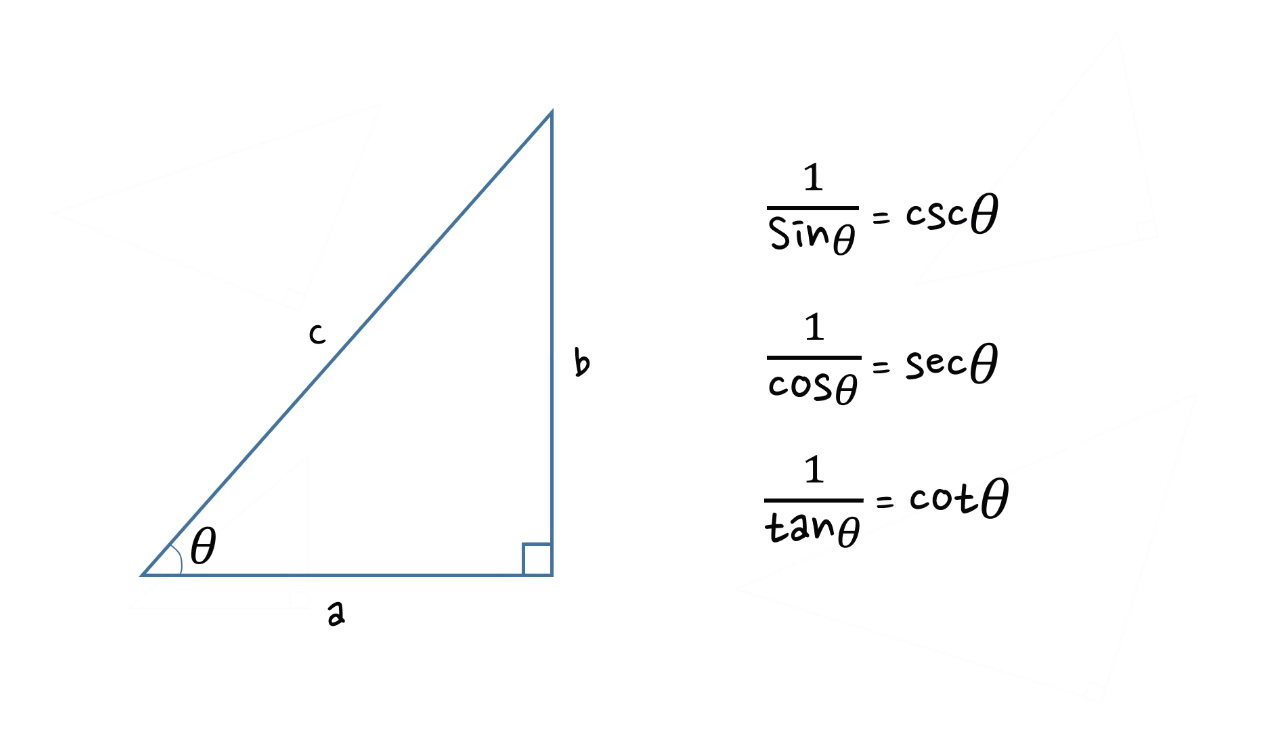
세 각의 크기가 각각 인 직각삼각형은 이등변삼각형이고, 세 각의 크기가 각각 인 직각삼각형의 빗변의 길이는 가장 짧은 변의 길이의 두 배라는 기하학적 사실과 피타고라스 정리를 이용하면 다음 결과를 얻게 된다.
sin 45° = 1/√2
cos 45° = 1/√2
tan 45° = 1
—————————
sin 30° = 1/2
cos 30° = √3/2
tan 30° = 1/√3
—————————
sin 60° = √3/2
cos 60° = 1/2
tan 60° = √3
2. 일반각에 대한 삼각함수
직각삼각형의 각은 0°와 90° 사이에 있으므로 위의 직각삼각형에 대한 삼각함수는 음의 각이나 90° 보다 큰 각에 대해서는 적용되지 않는다.
삼각함수를 일반각으로 확장하기 위해서는 좌표평면 위의 한 원을 살펴보는 것이 편리하다.
y좌표평면에서 원점 O를 중심으로 하고 반지름의 길이가 r인 원을 생각해 보자.
오른쪽 그림과 같이 이 원 위의 점 P(x,y)에 대해 동경 OP가 x축과 이루는 각의 크기를 θ라고 하면 위의 여섯 개의 삼각함수는 다음과 같이 정의된다.
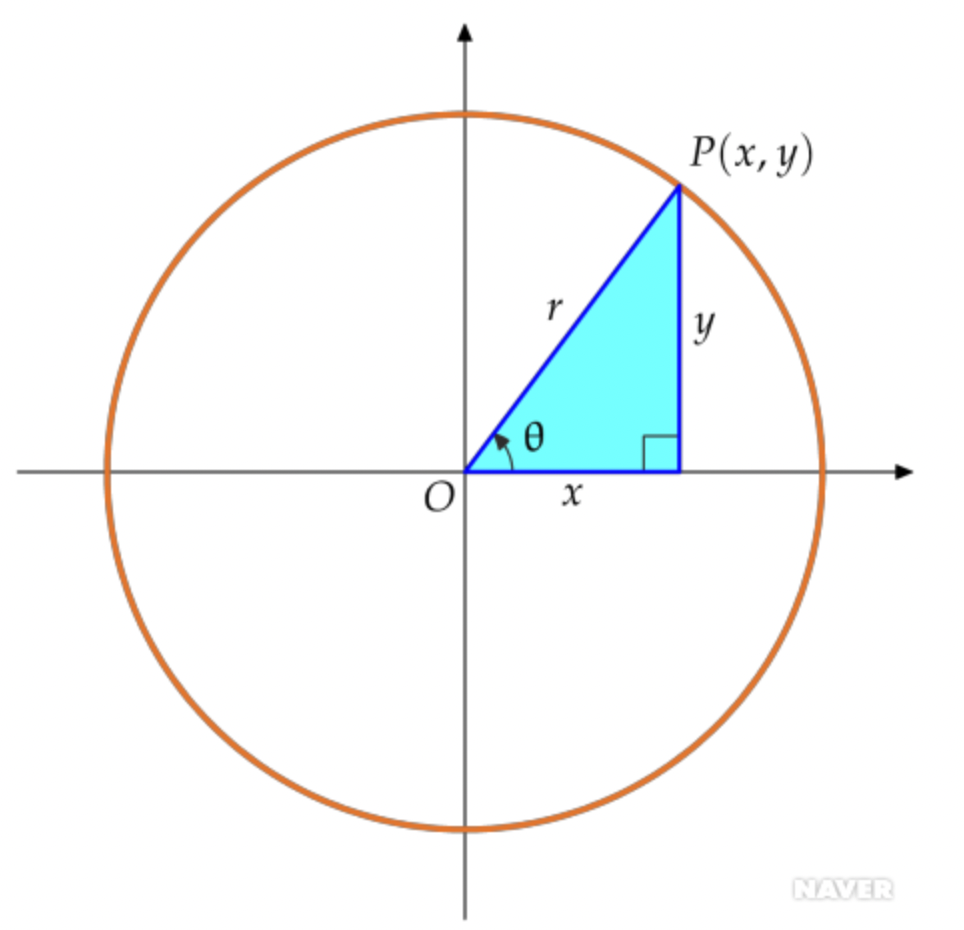
반지름 r 인 원에서의 삼각함수
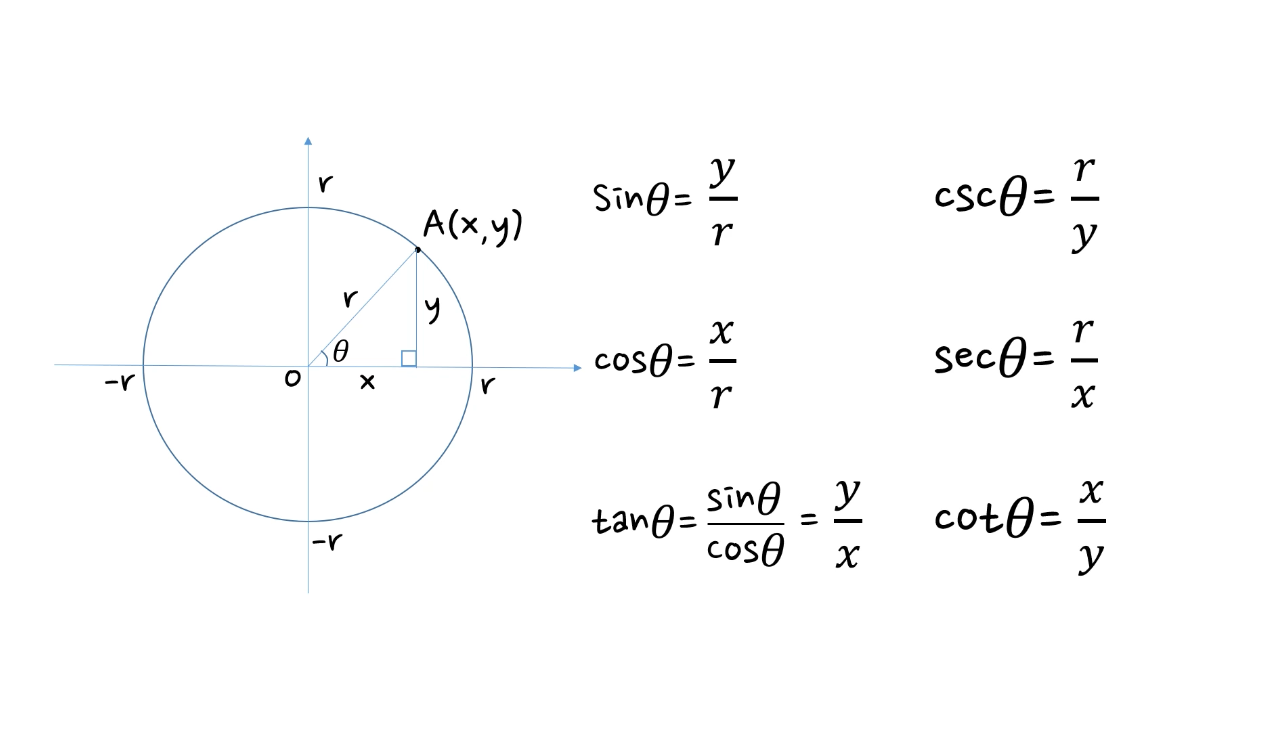
sin θ = y/r
cos θ = x/r
tan θ = y/x
역함수
csc θ = r/y
sec θ = r/x
cot θ = x/y
2-1. r의 값이 1일 때, 사인함수

sin θ = y
- 정의역은 실수 전체
- 주기 = 2π , 수식: f(x)=f(x+ 2π)
- 치역 = -1≤y≤ 1 (즉 최대값 1, 최소값 -1.)
- 원점대칭 홀함수
- 0 ~ 2π 까지 값의 변화 : 0 → 1 → 0 → -1 → 0
2-2. r의 값이 1일 때, 코사인함수

cos θ = x
- 정의역은 실수 전체
- 주기 = 2π , 수식: f(x)=f(x+ 2π)
- 치역 = -1≤y≤ 1 (즉 최대값 1, 최소값 -1.)
- y축대칭 짝함수
- 0 ~ 2π 까지 값의 변화 : 1 → 0 → -1 → 0 → 1
2-3. r의 값이 1일 때, 탄젠트함수
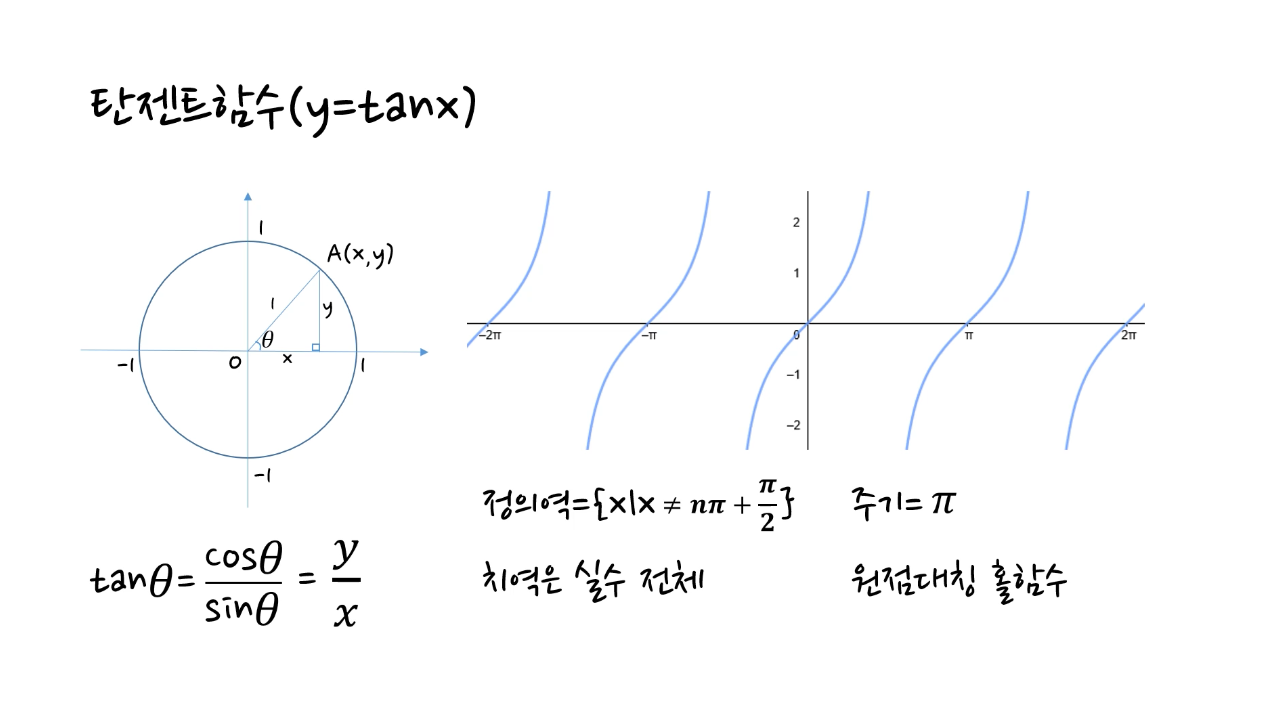
tan θ = cos θ / sin θ = y / x
- 정의역은 (nπ + π/2)를 제외한 실수 전체
- 주기 = π
- 치역은 실수 전체
- 원점대칭 홀함수
- 점근선 x = nπ + π/2 (n은 정수)
공부 출처 : 네이버 지식백과 삼각함수
